Geometry is really tricky. The best way to shape up is to make learning fun. In this blog, we share with you a super fun (and delicious!) way to learn how to work out the volume of a cone. Like chocolate? Read on!

The volume of a cone, is the space inside or the capacity of the cone.

There is no “perfect way” to learn. Some people learn well by just observing, but most people have deeper learning by “doing” or “experiencing” something. By developing an understanding of something by experiencing it, rather than just being told it is so.

Ice-cream & Chocolate Sauce Experiment

1. Engage

• In class today, we’re going to have ice-cream and chocolate sauce! The chocolate sauce serving can either be in a cylinder-shaped cup or a cone-shaped cup.
• You need to explore which option will give you more chocolate sauce deliciousness, and exactly how MUCH more, or LESS sauce you’ll get, once you’ve made your choice!

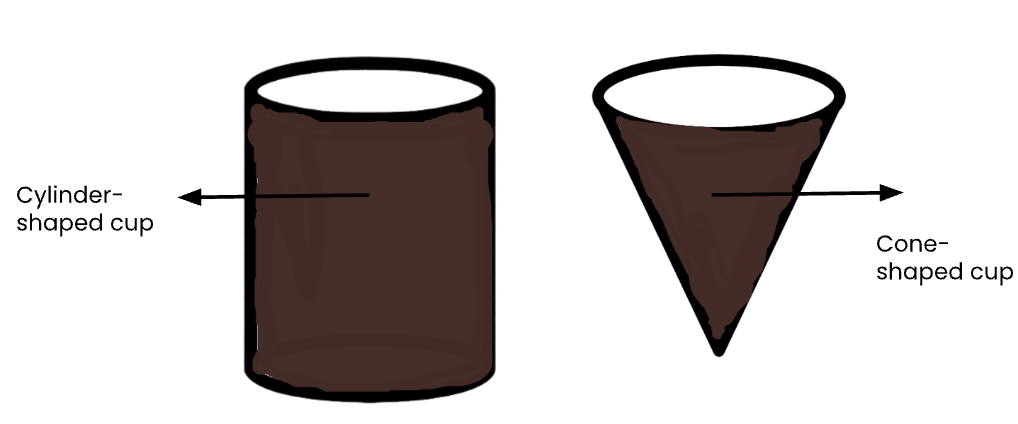
2. Explore

Using everyday materials, let’s make some connections to prior knowledge about a cylinder and see what we can learn about a cone.

What you’ll need: 

• a cylinder shape (glue stick lid)
• a cone (we’ll make one using contact plastic)
  

Your cone and your cylinder need to be the same height and have the same sized circle-shape at the top.

To make the cone:
Open this Kami doc: https://kami.app/GiK-EEN-XGN-hXE
Resize the cone net annotation (using the little purple circle in the bottom right of the annotation) to make the blue circle the same size as the circle shape of your glue stick lid.

Place a piece of paper over your screen and trace the cone net sector shape.

Cut out 2 sector shapes in plastic contact. It can be helpful to cut a larger flap on one of the sectors. Peel off the paper and stick the sticky sides together. If you didn’t do an extra flap, simply tape the sectors together into a cone shape, with cellotape or an extra piece of pealed contact.

Now you have a cylinder and a cone shape with the same height and the same circular open top.

• Explore how much coloured liquid each shape can hold. 
• Which can hold more?
• Can the one shape hold twice as much as the other?
• Can the one shape hold 3 times as much as the other?
• Can the one hold 4 time as much as the other?

3. Explain

Explain your discoveries about the volume of the cylinder and the cone. You can use a “What’s the big idea?” or “Lab report/Science experiment” Kami template.

4. Elaborate

Let’s build on what we know. We know that:

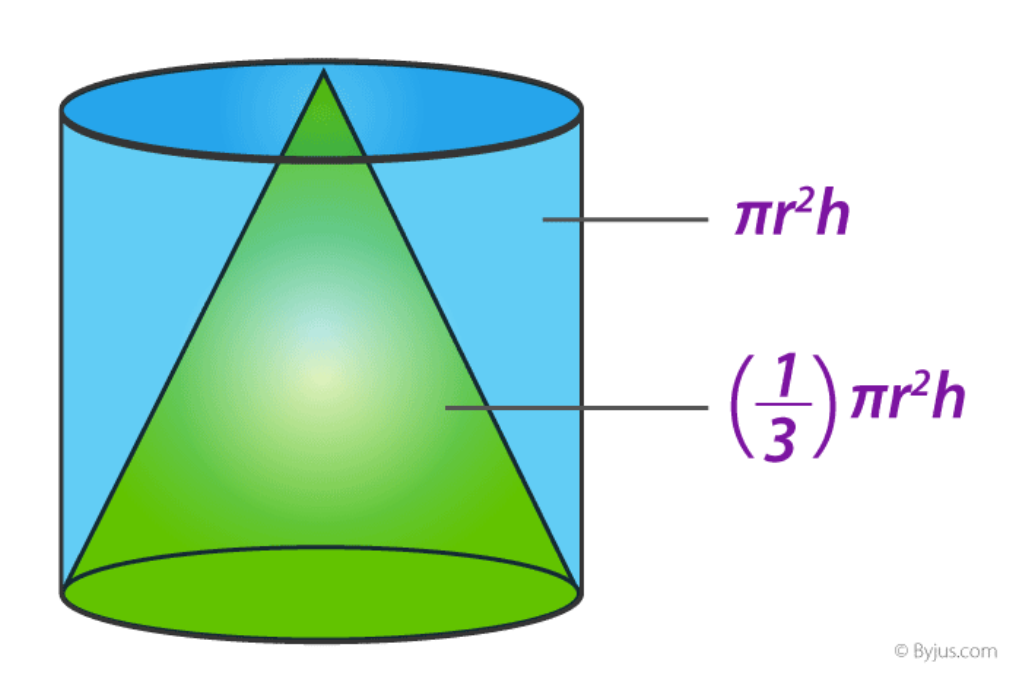
Volume of a Cylinder = Area of circular base x Height

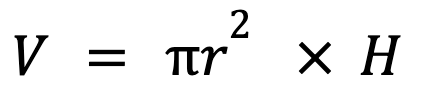
Volume of a Cone = ▁ x Area of circular base x Height

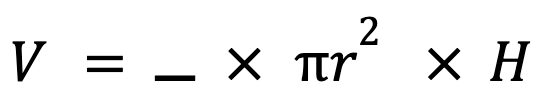
The volume of a cone with height H and radius r, is exactly one third of the volume of the smallest cylinder that fits inside it.

5. Evaluate

If the Volume of a Cylinder is 60 ㎤, the volume of a cone with the same circular base (or top) and same height would be …….?

If a cone has a volume of 15 ㎤, what is the Volume of the cylinder with the same circular base and height?

Wrapping Up

After a practical learning experience, it should be easy for you to make this decision. Here are 2 cups of delicious blueberry milkshake! Which one would you choose?

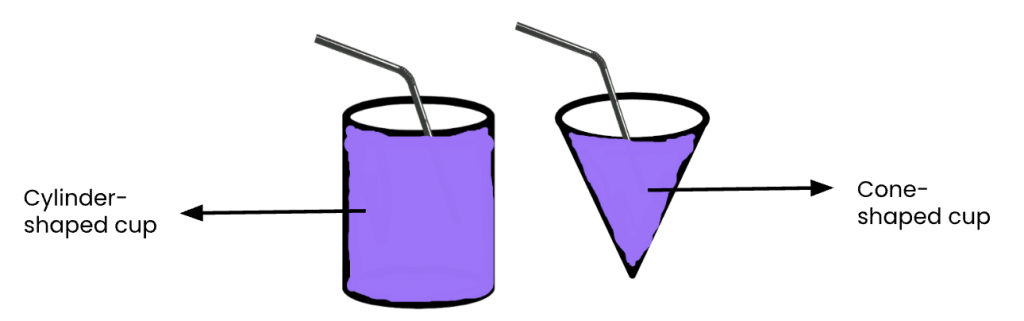
Yes! I’d choose the cylinder-shaped one too. There is more yummy milkshake in that one. Do you remember how MUCH more?

Volume

The amount of space inside a 3D shape is called the  volume of the shape. If we flip the cups over, we can see that both 3D shapes have the same size circular base.

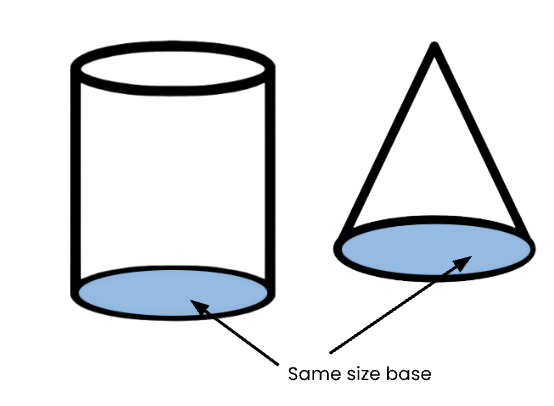
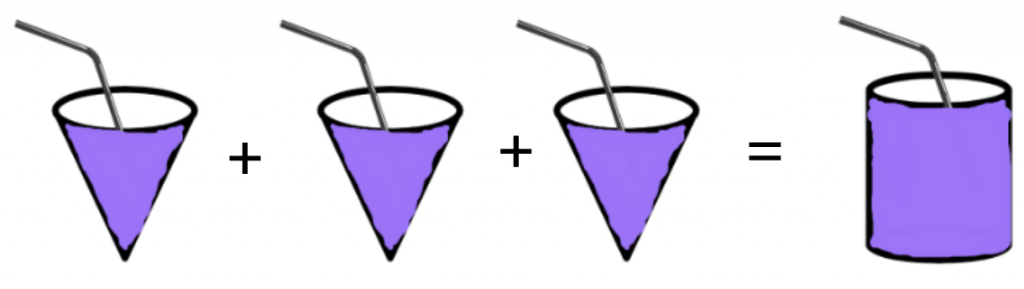
In our experiment, we discovered that the cylinder-shaped cup could hold exactly 3 times more than a cone shape with the same circular base and height.

The volume of the cone-shape is ⅓ of the volume of the cylinder.

Here is the formula for the volume of a right cone: 

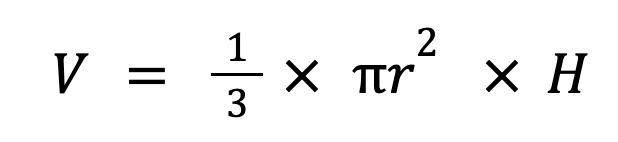
Hopefully you’ll agree that math is not only super fun, but it can also be delicious! If you’d like to learn how to find out the volume of a sphere, check out this blog.